算法

发表于 2024-06-07 更新于 2024-09-21 阅读次数：本文字数： 4.5k 阅读时长 ≈ 17 分钟

深度优先遍历（dfs）

const dfs = (node) => {
  dfs(node.child);
  console.log(node.value);
  dfs(node.sibling);
};

广度优先遍历（bfs）

const bfs = (node) => {
  const queue = [];
  if (node != null) {
    queue.push(node);
    while (queue.length > 0) {
      //出队
      const item = queue.shift();
      //操作
      console.log(item);
      const children = item.children;
      //子节点入队
      for (const child of children) {
        queue.push(child);
      }
    }
  }
};

找出两个数组的交集

例如：给定 nums1 = [1, 2, 2, 1]，nums2 = [2, 2]，返回 [2, 2]。

哈希表

const fn = (arr1, arr2) => {
  const map = new Map();
  const res = [];
  for (let i in arr1) {
    map.set(arr1[i], true);
  }

  for (let i in arr2) {
    if (map.has(arr2[i])) res.push(arr[i]);
  }

  return res;
};

依赖数组方法

const fn = (arr1, arr2) => {
  return arr1.filter((item) => arr2.includes(item));
};

移动零

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数。

const fn = (arr) => {
  let count = 0;
  for (let i in arr) {
    if (arr[i] === 0) {
      count++;
    } else {
      arr[i - count] = arr[i];
      arr[i] = 0;
    }
  }
};

最长连续序列

[0,3,7,2,5,8,4,6,0,1]

var longestConsecutive = function (nums) {
  let map = new Map();
  // 填充
  for (let i = 0; i < nums.length; i++) {
    map.set(nums[i], true);
  }
  let longestStreak = 0;
  // 判断
  for (let i = 0; i < nums.length; i++) {
    if (!map.get(nums[i] - 1)) {
      // 优化：没有比这个数小1的数，说明这个数最小
      // 没有上面这个判断也能行，但是会将所有的数都判断一遍
      let currentNum = nums[i];
      let currentStreak = 1;
      while (map.get(currentNum + 1)) {
        currentNum += 1;
        currentStreak += 1;
      }
      longestStreak = Math.max(longestStreak, currentStreak);
    }
  }
  return longestStreak;
};

排序

计数排序

中心思想是创建一个数组，然后取数组中最小值，然后每个数字减去最小值，然后根据减去最小值后的数字作为索引，如果有重复的，就将值+1,最后再遍历一遍数组，还原即可
索引+最小值 = 原数组的值
时间复杂度：O(n+k)
例：[2, 9, 6, 7, 4, 3, 1, 7,0,-1,-2]

const countingSort = (arr) => {
  let min = Math.min(...arr);
  const diff = -min;
  const countArr = [];
  const result = [];
  for (let i in arr) {
    // 一定是从零开始，最小值-自身一定是0
    countArr[arr[i] + diff] ?? (countArr[arr[i] + diff] = 0);
    countArr[arr[i] + diff]++;
  }
  for (let i in countArr) {
    const num = i - diff;
    result.push(...Array(countArr[i]).fill(num));
  }
  return result;
};

快速排序

取数组中间的数，遍历数组，小于这个数的放 left 数组，大于这个数放 right 数组，然后递归执行quickSort(left).concat([middle], quickSort(right));
时间复杂度：O(nlogn)
例：[2, 9, 6, 7, 4, 3, 1, 7]

const quickSort = (arr) => {
  if (arr.length <= 1) return arr;
  const index = Math.floor(arr.length / 2);
  const left = [],
    right = [];
  const middle = arr.splice(index, 1)[0];
  for (let i in arr) {
    if (arr[i] < middle) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([middle], quickSort(right));
};

快速排序时间复杂度，最坏情况是什么情况，什么情况下 n 方？

O(nlogn)
最坏情况时间复杂度是 O(n^2)。最坏情况通常发生在每次选择的中间数是数组中的最大或最小元素。这样每次分区后的一部分数组是空的，而另一部分包含剩余的所有元素，这样导致每次分区都需要 O(n) 的时间，而递归深度变成 O(n)，最终时间复杂度为 O(n^2)。
当数组已经有序（升序或降序），并且每次选择的枢轴是第一个元素或最后一个元素时，最坏情况会发生。当数组中所有元素都相同时，选择任何一个元素作为枢轴也会导致最坏情况。

归并排序

将数组拆成两半，递归执行，拆到只有一个元素，然后左右对比，组成数组返回。
时间复杂度: O(nlogn)

const merge = (arr1, arr2) => {
  const result = [];
  while (arr1.length && arr2.length) {
    // 左右两边都是排过序的数组，第一位一定是最小值
    if (arr1[0] < arr2[0]) {
      result.push(arr1.shift());
    } else {
      result.push(arr2.shift());
    }
  }

  if (arr1.length) {
    result.push(...arr1);
  }
  if (arr2.length) {
    result.push(...arr2);
  }
  return result;
};

const mergeSort = (arr) => {
  if (arr.length <= 1) return arr;
  const mid = Math.floor(arr.length / 2);

  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));
  return merge(left, right);
};

插入排序

数组每一项都和前面的数组进行比较，如果比前面的小，则交换位置
时间复杂度: O(n*n)

const insertionSort = (arr) => {
  for (let i in arr) {
    let preIndex = i - 1;
    while (preIndex >= 0 && arr[preIndex] > cur) {
      arr[preIndex + 1] = arr[preIndex--];
    }
    arr[preIndex + 1] = cur;
  }
  return arr;
};

选择排序

第一层循环选择一个，第二层循环选择第一层索引+1，比较，如果第一层的大于第二层的，则交换位置
时间复杂度O(n*n)

let selectSort = function (arr, flag = 0) {
  let len = arr.length,
    temp = 0; // 一共需要排序len-1次

  for (let i = 0; i < len - 1; i++) {
    temp = i;
    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[temp]) temp = j; // 更新索引
    } // 每一趟保证第i位为最小值
    if (temp !== i) {
      // 交换位置
      [arr[i], arr[temp]] = [arr[temp], arr[i]];
    }
  }

  return flag ? arr.reverse() : arr;
};

动态规划

核心思想就是找到一个状态转移方程，然后根据状态转移方程推导出状态转移方程

分割等和子集

给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

题解

01 背包解法

function canPartition(nums) {
  const sum = nums.reduce((pre, cur) => pre + cur);
  if (sum % 2 === 1) return false;
  const bagSize = sum / 2;
  const goodsNum = nums.length;
  const dp = new Array(bagSize + 1).fill(0);
  for (let i = 0; i < goodsNum; i++) {
    for (let j = bagSize; j >= nums[i]; j--) {
      dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
    }
  }
  return dp[bagSize] === bagSize;
}

记忆优化递归

原文题解
思路：每次向下递归都有两个选择：选和不选

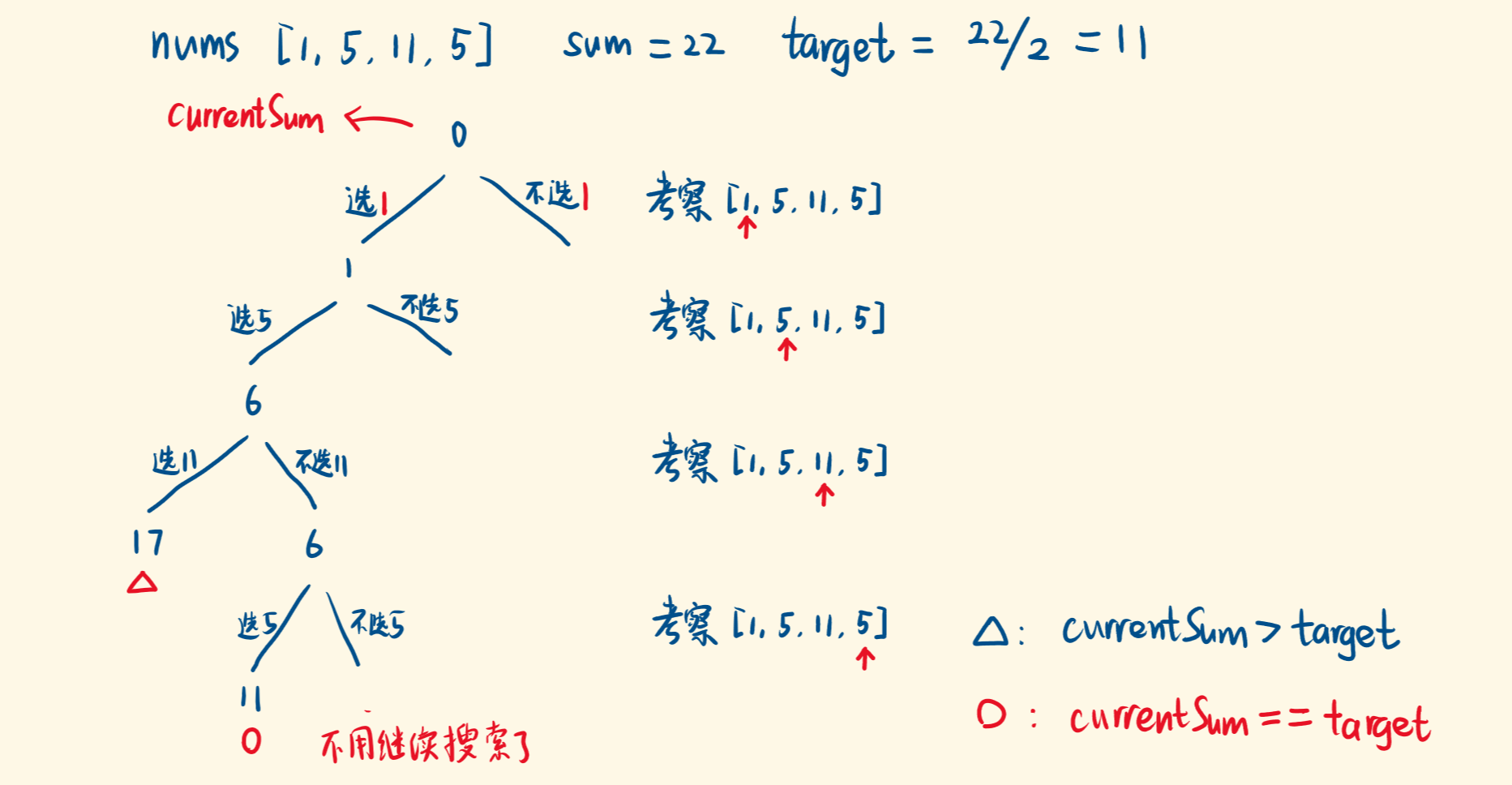
alt text
先看不包含记忆优化的递归（超时）。

const canPartition = (nums) => {
  let sum = 0;
  for (const n of nums) {
    // 求数组和
    sum += n;
  }
  if (sum % 2 != 0) return false; // 如果 sum 为奇数，直接返回 false

  const target = sum / 2; // 目标和

  // curSum是当前累加和，i是指针
  const dfs = (curSum, i) => {
    if (i == nums.length || curSum > target) {
      // 递归的出口
      return false;
    }
    if (curSum == target) {
      // 递归的出口
      return true;
    }
    // 选nums[i]，当前和变为curSum+nums[i]，考察的指针移动一位
    // 不选nums[i]，当前和还是curSum，考察的指针移动一位
    return dfs(curSum + nums[i], i + 1) || dfs(curSum, i + 1);
  };

  return dfs(0, 0); // 递归的入口，当前和为0，指针为0
};

加上记忆优化，将子问题缓存，遇到将重复的直接使用缓存，不再继续递归

const canPartition = (nums) => {
  let sum = 0;
  for (const n of nums) {
    // 求数组和
    sum += n;
  }
  if (sum % 2 != 0) return false; // 如果 sum 为奇数，直接返回 false
  const memo = new Map();
  const target = sum / 2; // 目标和

  const dfs = (curSum, i) => {
    // curSum是当前累加和，i是指针
    if (i == nums.length || curSum > target) {
      // 递归的出口
      return false;
    }
    if (curSum == target) {
      // 递归的出口
      return true;
    }
    const key = curSum + "&" + i; // 描述一个问题的key
    if (memo.has(key)) {
      // 如果memo中有对应的缓存值，直接使用
      return memo.get(key);
    }
    const res = dfs(curSum + nums[i], i + 1) || dfs(curSum, i + 1);
    memo.set(key, res); // 计算的结果存入memo
    return res;
  };

  return dfs(0, 0); // 递归的入口，当前和为0，指针为0
};

最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

示例 1：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：
输入：nums = [7,7,7,7,7,7,7]
输出：1

i是 nums 中每一项，j 是 i 的前一项，如果要满足递增，则nums[i] > nums[j]且i>j，转化一下就是求dp[i] = max(dp[j]) + 1 dp[i]就是子串长度，+1是把i自身这一项给算上

var lengthOfLIS = function (nums) {
  let n = nums.length;
  if (n === 0) return 0;

  let dp = new Array(n).fill(1);

  for (let i = 0; i < n; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }
  }

  return Math.max(...dp);
};

三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点在这里指的是下标与上一层结点下标相同或者等于上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：
输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
      2
    3 4
  6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：
输入：triangle = [[-10]]
输出：-10
题解

思路：从上往下来看，下面的数组未知，无法选择路径，所以从下往上看，倒数第二行开始。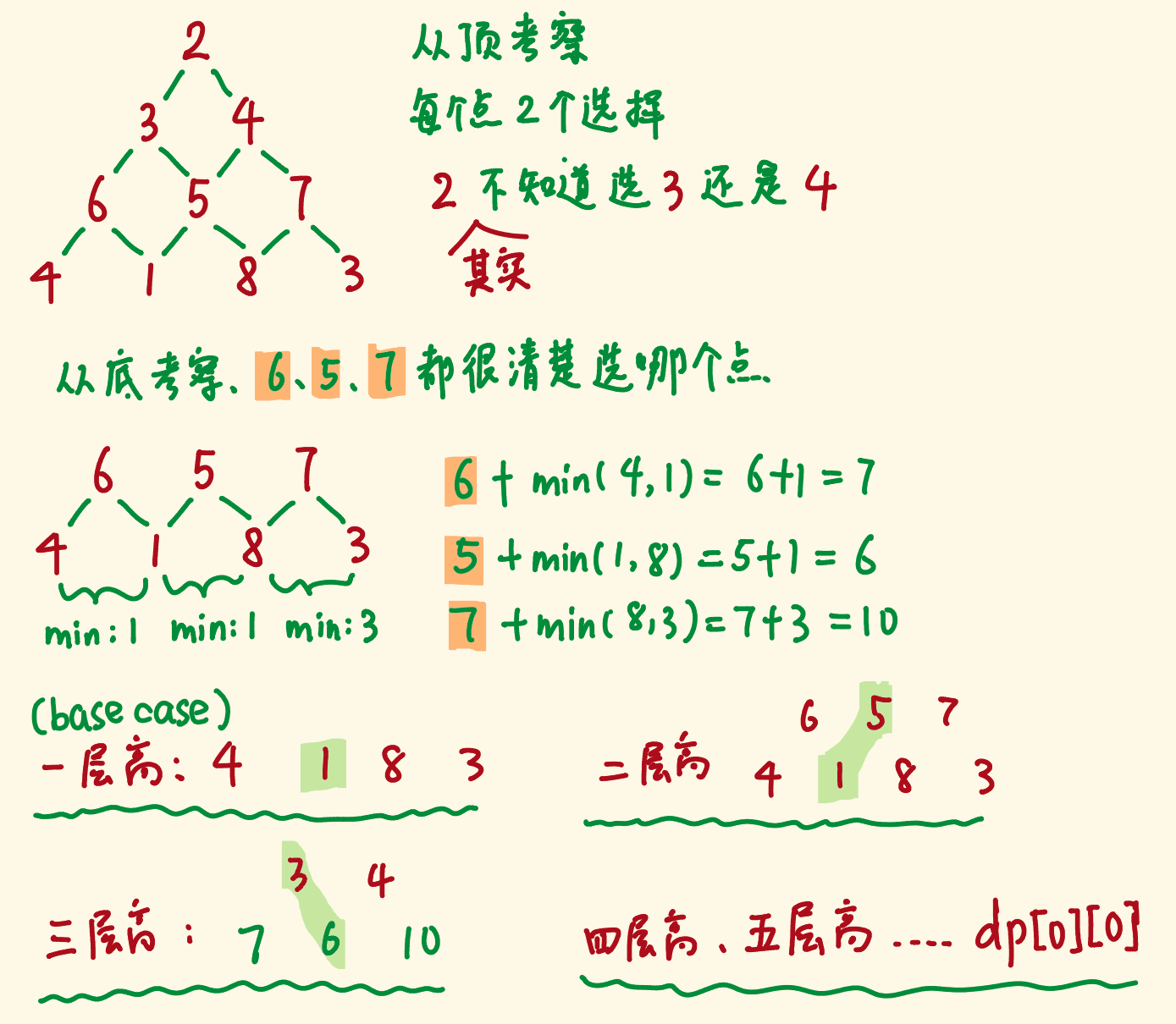
alt text

const minimumTotal = (triangle) => {
  const bottom = triangle[triangle.length - 1];
  const dp = new Array(bottom.length);
  // base case 是最后一行
  for (let i = 0; i < dp.length; i++) {
    dp[i] = bottom[i];
  }
  // 从倒数第二列开始迭代
  for (let i = dp.length - 2; i >= 0; i--) {
    for (let j = 0; j < triangle[i].length; j++) {
      // 算0 和 1索引的最小值+上一层就是新值
      dp[j] = Math.min(dp[j], dp[j + 1]) + triangle[i][j];
    }
  }
  return dp[0];
};

环状链表

判断是否有环

哈希表

var hasCycle = (head) => {
  let map = new Map();
  while (head) {
    if (map.has(head)) return true; //如果当前节点在map中存在就说明有环
    map.set(head, true); //否则就加入map
    head = head.next; //迭代节点
  }
  return false; //循环完成发现没有重复节点，说明没环
};

快慢指针

var hasCycle = (head) => {
  const fast = head;
  const slow = head;
  while (slow && fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) return true;
  }
  return false;
};

双指针

引用自labuladong

alt text

左右指针

盛水最多的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

示例 1：
输入：height = [1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
核心思想就是左右两个指针，哪边小就那个指针往内移动

var maxArea = function (height) {
  let max = 0;
  for (let i = 0, j = height.length - 1; i < j; ) {
    //双指针i，j循环height数组
    //i，j较小的那个先向内移动 如果高的指针先移动，那肯定不如当前的面积大
    const minHeight = height[i] < height[j] ? height[i++] : height[j--];
    const area = (j - i + 1) * minHeight; //计算面积
    max = Math.max(max, area); //更新最大面积
  }
  return max;
};

两数之和

思路就是两指针之和大于目标值，右边往内移动，否则左边往内移动

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。

示例 1：
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：
输入：nums = [3,2,4], target = 6
输出：[1,2]

const twoSum = (nums, target) => {
  let left = 0,
    right = nums.length - 1;

  while (left < right) {
    if (nums[left] + nums[right] === target) {
      return [left, right];
    }
    if (nums[left] + nums[right] > target) {
      right--;
    } else {
      left++;
    }
  }
};

三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。

示例 1：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例 2：
输入：nums = []
输出：[]

示例 3：
输入：nums = [0]
输出：[]

提示：
0 <= nums.length <= 3000
-105 <= nums[i] <= 105

const threeSum = function (nums) {
  const res = [];
  nums.sort((a, b) => a - b);
  console.log("nums", nums);
  for (let i = 0; i < nums.length; i++) {
    // 跟后一个值相同就跳过
    if (nums[i] === nums[i + 1]) continue;
    let left = i + 1,
      right = nums.length - 1;
    while (left < right) {
      // 跟后一个值相同就跳过
      if (nums[left + 1] === nums[left]) {
        left++;
        continue;
      }
      // 跟后一个值相同就跳过
      if (nums[right - 1] === nums[right]) {
        right--;
        continue;
      }
      const sum = nums[right] + nums[left] + nums[i];
      if (sum === 0) {
        res.push([nums[i], nums[left], nums[right]]);
        left++;
        right--;
      } else if (sum < 0) {
        left++;
      } else {
        right--;
      }
    }
  }
  return res;
};

求最接近的三数之和

思路：类似求三数之和，但是不需要判断是否重复，根据每次算出的总值判断是大于还是小于目标值，然后移动对应的指针

给定一个包括 n 个整数的数组 nums 和一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例：
输入：nums = [-1,2,1,-4], target = 1
输出：2

const threeSum = function (nums, target) {
  let result;
  nums.sort((a, b) => a - b);
  result = nums[0] + nums[1] + nums[nums.length - 1];
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] === nums[i + 1]) continue;
    let left = i + 1,
      right = nums.length - 1;

    while (left < right) {
      const sum = nums[right] + nums[left] + nums[i];

      const preDiff = Math.abs(result - target);
      const diff = Math.abs(sum - target);
      result = Math.min(preDiff, diff) === preDiff ? result : sum;

      if (diff === 0) return target;
      else if (sum > target) {
        right--;
      } else {
        left++;
      }
    }
  }
  return result;
};

快慢指针 / 滑动窗口

长度最小的子数组

思路：慢指针在第一层循环中，快指针在第二层循环中，当快指针遍历到 ≥s 时，慢指针移动一位，直到遍历结束。

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
示例：
输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

const minSubArrayLen = function (target, nums) {
  let min;
  for (let i = 0; i < nums.length; i++) {
    let left = i;
    let right = i + 1;
    let sum = nums[i];
    if (nums[i] >= target) return 1;
    while (right < nums.length) {
      sum += nums[right++];
      if (sum >= target) {
        // min初始为undefined
        if (min === undefined) min = right - left;
        else min = Math.min(min, right - left);
        // 已经找到这一轮的最小值了，可以推出，左指针进一位
        break;
      }
    }
  }
  return min;
};

无重复字符的最长子串

思路：两个指针，从同一位置开始遍历，使用 map 保存遍历过的字符，如果遍历到重复的，左指针移动并且删除掉 map 中重复的字符，直到不重复为止，记录最大长度；如果遍历到没有重复的移动右指针

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2:
输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。

const lengthOfLongestSubstring = function (s) {
  let max = (left = right = 0);
  let map = {};
  for (let i = 0; i < s.length; i++) {
    while (map[s[right]] && left < right) {
      map[s[left]] = false;
      left++;
    }
    map[s[right]] = true;
    max = Math.max(max, right - left + 1);
    right++;
  }
  return max;
};

最长回文子串

思路：定一个或两个中心（因为回文分奇偶，所以中心会有一个或者两个的情况），由中心往两边扩展，找到最长的回文子串

输入: “babad”
输出: “bab”

输入: “cbbd”
输出: “bb”

输入: “a”
输出: “a”

const longestPalindrome = function (s) {
  // 定义返回的最长回文子串
  let res = "";
  // 开始循环每一个字符
  for (let i = 0; i < s.length; i++) {
    // 当回文子串为奇数时，回文中点只有一位
    traverse(i, i);
    // 当回文子串为偶数时，回文中点有两位
    traverse(i, i + 1);
  }
  function traverse(left, right) {
    // 首先不能越界，其次两个元素要相等，然后m左移，n右移进行比较
    while (left >= 0 && right < s.length && s[left] === s[right]) {
      left--;
      right++;
    }
    // 比较当前回文字符串的长度是否比前面的回文字符串长度长，长则进行更新。
    // -1是因为要求上一轮的字符串长度，原本是right-left+1,但是最后一次while循环中left--,right++了
    if (right - left - 1 > res.length) {
      // +1是因为要求上一轮的字符串长度，将左指针+1，因为slice是闭区间，所以不需要+1
      res = s.slice(left + 1, right);
    }
  }
  return res;
};

500 个节点的完全二叉树有多少叶子节点，深度是多少

二叉树的第i层至多有2^(i − 1)个结点
深度为k的二叉树至多有2^k − 1个结点

2^9 − 1>=500，所以有9层。0

前8层都是满二叉树，前8层有2^8 − 1 = 255，所以第9层有500-255 = 245个。

245为奇数可知其父结点一定有单分支，其父结点个数为244 / 2+1＝123（其中有一个单分支结点）

第8层有2^(8 - 1)＝128个结点，其中叶子结点个数128-123＝5

第八层叶子节点+第九层节点 = 250个

队列和栈

滑动窗口最大值

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

思路： 使用一个双端队列（Deque）来存储当前窗口中元素的索引。队列中的索引按照对应元素从大到小的顺序排列，这样队列的头部始终是当前窗口中的最大值的索引。滑动窗口机制：对于数组中的每一个元素，我们首先移除那些已经滑出窗口的元素（通过检查索引是否超出窗口范围）。然后，我们从队尾开始移除队列中比当前元素小的所有元素，因为这些较小的元素不可能再成为当前窗口的最大值。最后，将当前元素的索引加入队尾。当窗口的大小达到 k 时，队列的头部元素就是当前窗口的最大值。

function maxSlidingWindow(nums, k) {
  const deque = [];
  const result = [];

  for (let i = 0; i < nums.length; i++) {
    // 将不在滑动窗口范围外的元素出队列
    // i - k + 1 是当前滑动窗口的左边界
    if (deque.length && deque[0] < i - k + 1) {
      deque.shift();
    }
    // 重复比较队尾和当前元素大小，移除队列中比当前元素小的元素，保持队列递减
    while (deque.length && nums[deque[deque.length - 1]] <= nums[i]) {
      deque.pop();
    }
    deque.push(i);
    // 只有遍历到nums前两位时不需要push结果
    if (i >= k - 1) {
      result.push(nums[deque[0]]);
    }
  }

  return result;
}

// 示例
console.log(maxSlidingWindow([1, 3, -1, -3, 5, 3, 6, 7], 3)); // [3,3,5,5,6,7]